High-dimensional learning is inherently complex.
DL, basically, is just a search for the proper parameters to make models fit datasets in a particular space.
The problem is that as the number of dimensions in said space increases, so does the required amount of training samples.
This is known as the curse of dimensionality and it’s one of machine learning’s most damning challenges.
The term COD doesn’t refer to one specific issue but, rather, describes various phenomena that occur when researchers organize, process, or analyze data in high-dimensional spaces.
Their common feature is that they all stem from this one law: a dimensionality increase inevitably leads to an enlargement of the input space to the point where the available dataset becomes sparse.
Gaining statistically sound results from any model in such circumstances requires an enormously high number of samples, and trying to obtain them – to get thousands or even millions of labeled data points – is a prohibitively costly approach to solving the problem.
And, no, simply projecting high-dimensional data into low-dimensional spaces to make it palatable isn’t an option: it leads to fidelity losses that are far too high for the resulting predictions to be valuable.
Luckily though, there is a saving grace – the regularities in the datasets.
The information we get from the physical world is typically just a bunch of semantically equivalent replicas of the same thing. And this notion of regularity, when encoded into a neural net architecture, allows us to reduce the search space of possible target functions and find the solution quicker.
In the machine learning community, this is called introducing inductive bias, and it’s one of the key principles of Geometric Deep Learning – the new paradigm we’ll cover today.
Geometric Deep Learning
Back a few years ago, the term GLM was synonymous with Graph Neural Networks i.e. models capable of handling non-Euclidean data (graphs, spheres, meshes, etc.)
Now, it is being used to describe any type of deep learning architecture that leverages geometric priors and the underlying structure of a dataset.
GDL Principles
#1 Symmetry Groups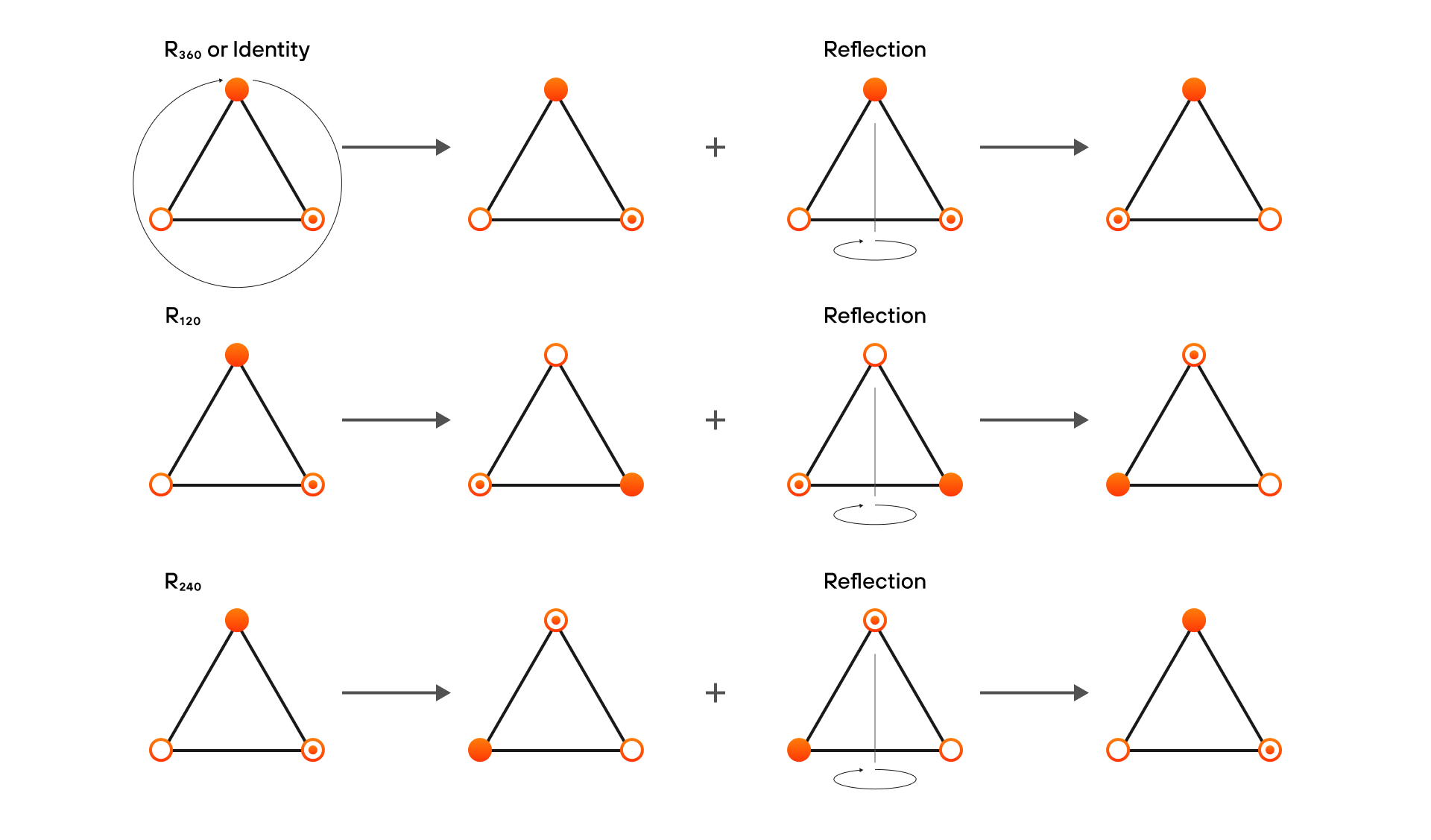 Assume that all high-dimensional data exists on some domains, which are just sets, possibly with an extra structure such as neighborhoods. And these domains impose certain limitations on the class of transformations that can be applied to the datasets.
Assume that all high-dimensional data exists on some domains, which are just sets, possibly with an extra structure such as neighborhoods. And these domains impose certain limitations on the class of transformations that can be applied to the datasets.
Namely, we only use specific types of transformations in Geometric Deep Learning called symmetries.
Symmetries are modifications that do not change the object.
In DL, for example, there are symmetries of weights, which allow the processing of graphs independently of isomorphism (if we swap two neurons within a graph neural network, it’ll still remain graph isomorphic.)
There are also symmetries of label functions, which enable us to work on visual data independently of shifts and rotations (rotate the image of a dog all you want – a trained CNN will still output the label “dog”.)
Note: In deep learning, we typically give the models lots of training samples representing semantically equivalent transformations of the same object until they “realize” that these inputs should all be labeled the same way. But if the algorithms knew all the symmetries of a certain class from the get-go, they’d be able to classify the object accurately after seeing just one training example.
In GDL, symmetries are used to preserve the structure of the domains.
They include permutations that keep the membership of a set intact and, as we’ve just mentioned, reflections/rotations that don’t affect angles or Euclidean distances.
Symmetry transformations are characterized by group theory which describes precisely what properties they should process, including:
- Composability. If we have two functions that preserve the object’s structure, we should be able to apply them one after another and get as a result a third function that also leaves the object unchanged.
- Invertibility. The function we’re looking for must have an inverse, otherwise, we’d lose information from the input signal while processing it.
- Identity. The identity function just returns the same value the object had, without modifying it. So, by definition, it’s a symmetry.
There are two types of symmetry-resistant functions: the invariant and the equivariant ones.
If we apply any element of the symmetry group to any part of the input (or the entire signal) and it doesn’t affect the end result – the function is invariant. Image classification with a CNN is a bright example of this – if we shift the image, or rotate it, we still want the network to know which category to put it under.
However, if we just want a prediction over a single node as opposed to the entire domain, invariant functions can be harmful as they can irreparably damage an element’s identity.
In this case, a more fine-grained equivariant function is needed. It will change the output to some degree but only in the same way it modified the input.
So, for instance, in an image segmentation problem, after shifting some part of the input image, we’ll get the segmentation mask that includes exactly the same shift.
#2 Scale Separation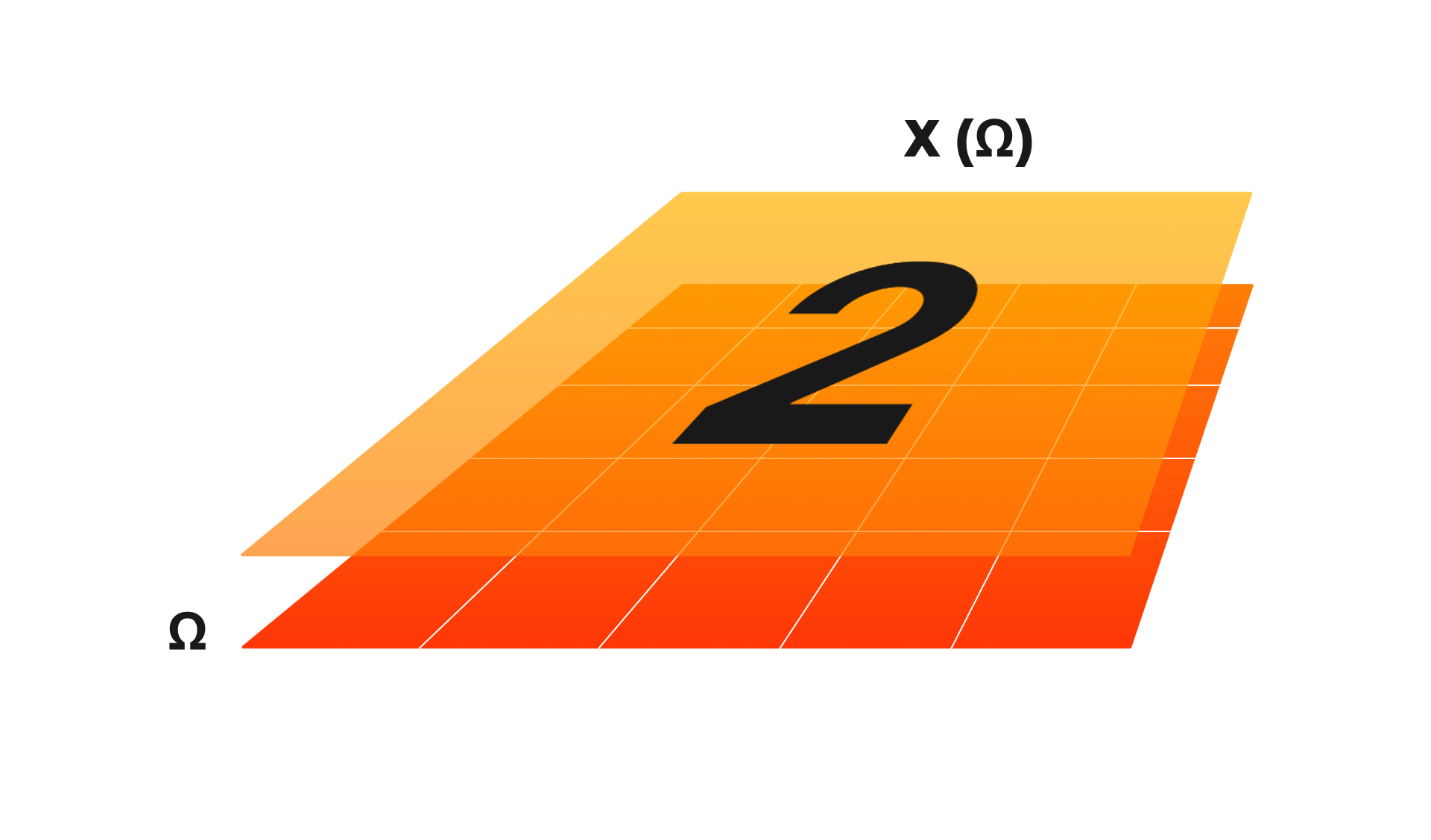 Using symmetries limits greatly the number of functions we have to look through when trying to find a fit for a high-dimensional dataset, but, sometimes, we’re unable to apply them in pure form as real-world inputs tend to be very susceptible to distortions, and all kinds of noise.
Using symmetries limits greatly the number of functions we have to look through when trying to find a fit for a high-dimensional dataset, but, sometimes, we’re unable to apply them in pure form as real-world inputs tend to be very susceptible to distortions, and all kinds of noise.
To fight this, GDL introduces another important constraint – scale separation – on top of the symmetry rule. This helps to preserve the stability of an input signal even after it was distorted.
The principle states that we should use local operations, which won’t propagate errors globally, to model large-scale modifications. Applying scale separation means any deformations in the input will be contained to a certain region and thus not affect the overall processing and the end prediction.
This approach has been used successfully in modern CNNs, in which at every layer a small (typically 3×3) matrix slides through the regions of the input pixel grid to produce activation functions for the next layer.
GDL ingredients
Geometric deep learning gives us a unification framework for all existing advanced neural nets as well as a formula for constructing future NN architectures for high-dimensional learning.
GDL’s building blocks are:
- linear equivariance layers
- non-linear activation functions
- local pooling layers (that help to establish geometric stability by containing noise in the input)
- invariance layers (global pooling).
GDL applications
Though the ML community as a whole is still somewhat reluctant to aim research efforts at real-world problems, GDL has already proved its significance and practicality. Here are some examples:
- Google uses a deep reinforcement learning model that is able to process graph data for placement optimization and chip design cycle shortening. The network, according to the authors, can achieve optimum placement of chip circuitry and produce designs that always take into account the latest trends, are smaller and cost a lot less than the man-made ones. It also performs the tasks significantly faster than any human expert possibly could.
- DeepMind’s AlphaFold has resolved one of the most significant biological problems of the last century – protein folding. Before it emerged, the issue was considered unsolvable and hampered advances in medicine and biotechnology. Now, AplhaFold 2, which has swapped convolutions for graphs and is attention-based, can even predict protein structures in cases where no similar structures have been researched before, with atomic accuracy. The method leverages existing knowledge of proteins both from physics and biology, incorporates multi-sequence alignments, and outperforms greatly all the other models trained for this specific task.
- Jonathan M. Stokes et al. trained a neural net to predict molecules with antibacterial properties which brought the researchers to the discovery of halicin – a unique molecule that’s effective against a wide range of pathogens while being structurally different from all conventional antibiotics.
- UberEats uses a particular type of GNN architecture, GraphSage, to display food recommendations that will most likely appeal to each individual user. What the GNN does is concatenate the information of the graph nodes and their neighbors and constrict the number of the sampled nodes to those within a 1- 2-hop distance from the node of interest. This approach allows UberEats’ recommender system to learn from graphs comprising billions of nodes and drastically enhance the quality and relevance of its food and restaurant suggestions.
Summing Up
Geometric Deep Learning does three things:
- introduces some geometrical rules for the simplification of high-dimensional learning and for tackling the input order problem through the principles of invariance and equivariance;
- attempts to provide a formal unification for a broad class of existing machine learning problems;
- describes a template or a series of building blocks for the design of future advanced neural networks.
Using this new, principled way to approach ML model building can help apply promising neural architectures in a wide range of fields – from pharma to industry, to healthcare, to social science, and more.
Want to explore the capabilities of Graph Neural Networks in the context of your specific business problem? Reach out to our data science expert right now!


 Assume that all high-dimensional data exists on some domains, which are just sets, possibly with an extra structure such as neighborhoods. And these domains impose certain limitations on the class of transformations that can be applied to the datasets.
Assume that all high-dimensional data exists on some domains, which are just sets, possibly with an extra structure such as neighborhoods. And these domains impose certain limitations on the class of transformations that can be applied to the datasets.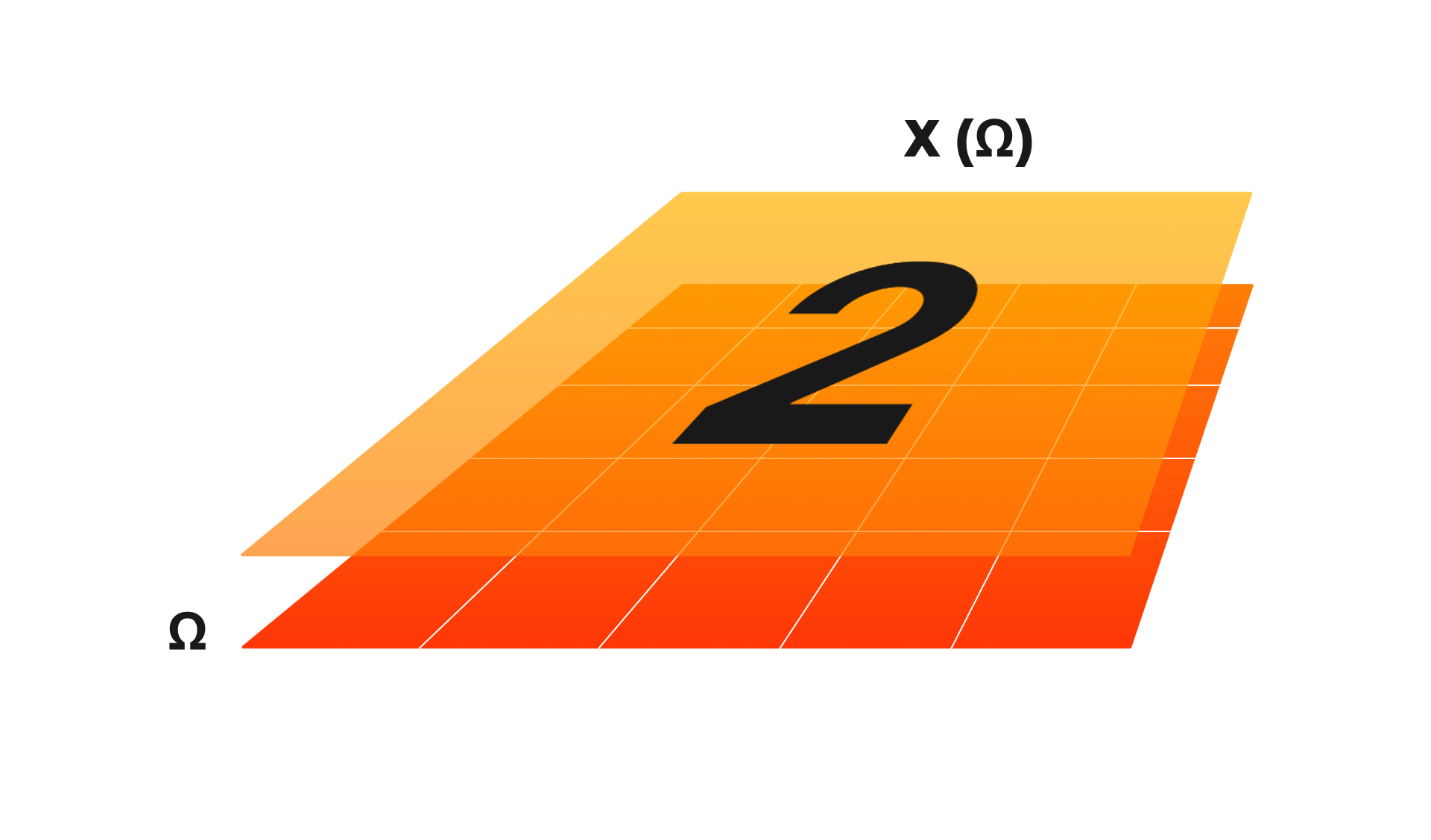 Using symmetries limits greatly the number of functions we have to look through when trying to find a fit for a high-dimensional dataset, but, sometimes, we’re unable to apply them in pure form as real-world inputs tend to be very susceptible to distortions, and all kinds of noise.
Using symmetries limits greatly the number of functions we have to look through when trying to find a fit for a high-dimensional dataset, but, sometimes, we’re unable to apply them in pure form as real-world inputs tend to be very susceptible to distortions, and all kinds of noise.






